吉法师的博客

一、入门

常见的时间复杂度类型

1.O(1)

 int i = 8;
 int j = 6;
 int sum = i + j;

代码的运行次数不会随着n进行变化，比如没有进入循环，所以是O(1)级别

2.O(logn)、O(nlogn)

 i=1;
 while (i <= n)  {
   i = i * 2;
 }

比如以下这段代码，就是O(log3n)。

i=1;
while (i <= n)  {
  i = i * 3;
}

我们知道，对数之间是可以互相转换的，log3n 就等于 log32 * log2n，所以 O(log3n) = O(C * log2n)，其中 C=log32 是一个常量。基于我们前面的一个理论：在采用大 O 标记复杂度的时候，可以忽略系数，即 O(Cf(n)) = O(f(n))。所以，O(log2n) 就等于 O(log3n)。因此，在对数阶时间复杂度的表示方法里，我们忽略对数的“底”，统一表示为 O(logn)。

3.O(m+n)、O(m*n)

int cal(int m, int n) {
 int sum_1 = 0;
 int i = 1;
 for (; i < m; ++i) {
   sum_1 = sum_1 + i;
 }

 int sum_2 = 0;
 int j = 1;
 for (; j < n; ++j) {
   sum_2 = sum_2 + j;
 }

 return sum_1 + sum_2;
}

从代码中可以看出，m 和 n 是表示两个数据规模。我们无法事先评估 m 和 n 谁的量级大，所以我们在表示复杂度的时候，就不能简单地利用加法法则，省略掉其中一个。

所以，上面代码的时间复杂度就是 O(m+n)。针对这种情况，原来的加法法则就不正确了，我们需要将加法规则改为：T1(m) + T2(n) = O(f(m) + g(n))。但是乘法法则继续有效：T1(m)*T2(n) = O(f(m) * f(n))。

常见的空间复杂度类型

void print(int n) {
  int i = 0;
  int[] a = new int[n];
  for (i; i <n; ++i) {
    a[i] = i * i;
  }

  for (i = n-1; i >= 0; --i) {
    print out a[i]
  }
}

跟时间复杂度分析一样，我们可以看到，第 2 行代码中，我们申请了一个空间存储变量 i，但是它是常量阶的，跟数据规模 n 没有关系，所以我们可以忽略。 第 3 行申请了一个大小为 n 的 int 类型数组，除此之外，剩下的代码都没有占用更多的空间，所以整段代码的空间复杂度就是 O(n)。

二、基础

1.基于链表的LRU缓存淘汰算法

LRU：最近最少使用

我们维护一个有序单链表，越靠近链表尾部的结点是越早之前访问的。

当有一个新的数据被访问时，我们从链表头开始顺序遍历链表。

1. 如果此数据之前已经被缓存在链表中了，我们遍历得到这个数据对应的结点，并将其从原来的位置删除，然后再插入到链表的头部。

2. 如果此数据没有在缓存链表中，又可以分为两种情况：如果此时缓存未满，则将此结点直接插入到链表的头部；如果此时缓存已满，则链表尾结点删除，将新的数据结点插入链表的头部。

这样就实现了一个LRU算法。

2.栈在括号匹配中的作用

当遇到左括号的时候，压入栈，遇到右括号的时候出栈。空栈遇到右括号的话，则表示这个括号对已经不匹配了。

只要最后看栈中的元素是否为空，就能知道括号是否匹配了。

栈也可以实现浏览器的前进后退，前进的时候在后退栈压入数据（同时可能需要出栈），后退的时候出栈，入前进栈。前进时前进栈出栈，入后退栈。

3.队列的用途 阻塞队列

简单来说就是资源比较紧张的时候，会判断队列内是否存放了东西，如果队列为空的话，会一直阻塞到队列内有值才放行。但这样实现的话效率会低一点。

4.递归的简单理解

其实就是去电影院问座位号，坐在中间的人自己也不知道，需要传递到第一排问到结果，再传回来，递和归的过程。

5.为什么Redis用的是跳表而不是红黑树呢？

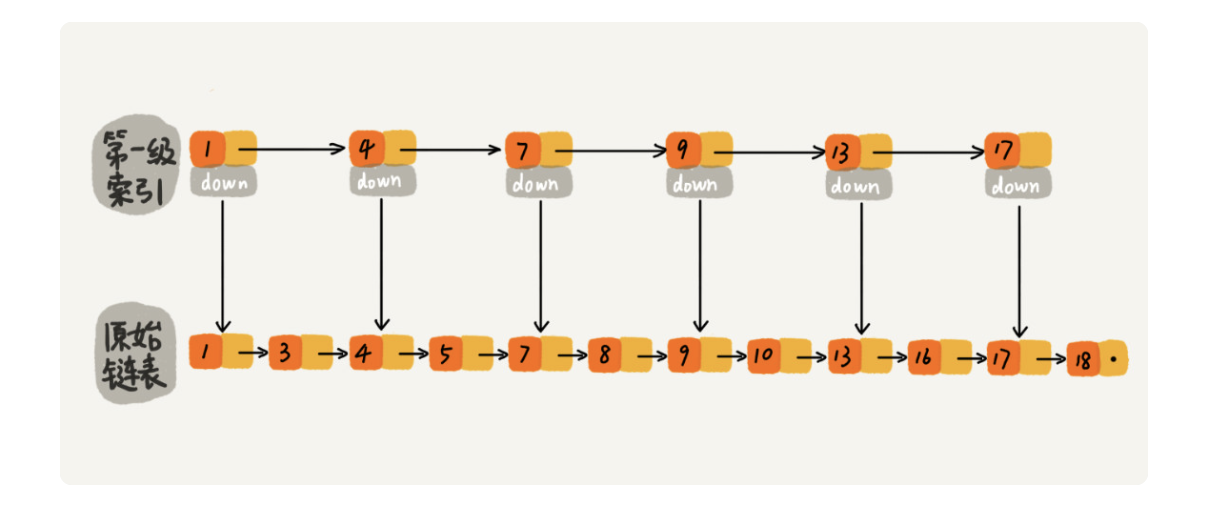
如果我们现在要查找某个结点，比如 16。我们可以先在索引层遍历，当遍历到索引层中值为 13 的结点时，我们发现下一个结点是 17，那要查找的结点 16 肯定就在这两个结点之间。

然后我们通过索引层结点的 down 指针，下降到原始链表这一层，继续遍历。这个时候，我们只需要再遍历 2 个结点，就可以找到值等于 16 的这个结点了。这样，原来如果要查找 16，需要遍历 10 个结点，现在只需要遍历 7 个结点。

简而言之

跳表和时间复杂度几乎和红黑树一样，而且实现起来简单。

6.检查拼写错误，用什么数据结构实现？

常用的英文单词有 20 万个左右，假设单词的平均长度是 10 个字母，平均一个单词占用 10 个字节的内存空间，那 20 万英文单词大约占 2MB 的存储空间，就算放大 10 倍也就是 20MB。对于现在的计算机来说，这个大小完全可以放在内存里面。所以我们可以用散列表来存储整个英文单词词典。

也就是哈希表，通过这个输入的单词的哈希值，在哈希表中寻找是否有匹配的值，若没有则说明是一个错误的拼写。

哈希表解决冲突，暂时掌握拉链法。

7.哈希算法对数据分片和负载均衡的处理。

比如ip地址相同的请求，通过计算哈希值取模，一定可以分配到同一台服务器进行处理。

对于关键词的次数统计等问题，可以通过哈希值计算后，分配给每个计算机进行处理，而不是堆给一台服务器。

分布式系统，也许会大量使用哈希算法来进行负载方面的处理。

8.红黑树部分

一棵合格的红黑树需要满足这样几个要求：

• 根节点是黑色的；每个叶子节点都是黑色的空节点（NIL），也就是说，叶子节点不存储数据；
• 任何相邻的节点都不能同时为红色，也就是说，红色节点是被黑色节点隔开的；
• 每个节点，从该节点到达其可达叶子节点的所有路径，都包含相同数目的黑色节点。

红黑树是一种平衡二叉查找树。它是为了解决普通二叉查找树在数据更新的过程中，复杂度退化的问题而产生的。红黑树的高度近似 log2n，所以它是近似平衡，插入、删除、查找操作的时间复杂度都是 O(logn)。

因为红黑树是一种性能非常稳定的二叉查找树，所以，在工程中，但凡是用到动态插入、删除、查找数据的场景，都可以用到它。不过，它实现起来比较复杂，如果自己写代码实现，难度会有些高，这个时候，我们其实更倾向用跳表来替代它。

红黑树的效率和跳跃链表相差并不大。

9.完全二叉树、满二叉树和堆

完全二叉树是每个节点要么是叶子，要么就一定有左右子树。

满二叉树是除了最后一层，其他的必须有左右子树和叶子，最后一层节点靠左排列。

堆：堆是一个完全二叉树；堆中每一个节点的值都必须大于等于（或小于等于）其子树中每个节点的值。

对于每个节点的值都大于等于子树中每个节点值的堆，我们叫做“大顶堆”。对于每个节点的值都小于等于子树中每个节点值的堆，我们叫做“小顶堆”。

10.关于第k大问题

若要维护一个排行榜，最适合用堆这个数据结构，通过每次不断地堆化，若最后取前十位，也只需要从大顶堆开始遍历即可。

11.字符串匹配算法

• BM算法

BF 是 Brute Force 的缩写，中文叫作暴力匹配算法。

• RK算法

RK 算法的全称叫 Rabin-Karp 算法，是由它的两位发明者 Rabin 和 Karp 的名字来命名的。

RK 算法的思路是这样的：我们通过哈希算法对主串中的 n-m+1 个子串分别求哈希值，然后逐个与模式串的哈希值比较大小。如果某个子串的哈希值与模式串相等，那就说明对应的子串和模式串匹配了（这里先不考虑哈希冲突的问题，后面我们会讲到）。因为哈希值是一个数字，数字之间比较是否相等是非常快速的，所以模式串和子串比较的效率就提高了。

但是RK算法要应对各种语言的字符并不容易

• BM算法

BM（Boyer-Moore）算法包含两部分，分别是坏字符规则（bad character rule）和好后缀规则（good suffix shift）。

1. 坏字符规则

我们从模式串的末尾往前倒着匹配，当我们发现某个字符没法匹配的时候。我们把这个没有匹配的字符叫作坏字符（主串中的字符）。

我们拿坏字符 c 在模式串中查找，发现模式串中并不存在这个字符，也就是说，字符 c 与模式串中的任何字符都不可能匹配。这个时候，我们可以将模式串直接往后滑动三位，将模式串滑动到 c 后面的位置，再从模式串的末尾字符开始比较。

这个时候，我们发现，模式串中最后一个字符 d，还是无法跟主串中的 a 匹配，这个时候，还能将模式串往后滑动三位吗？答案是不行的。因为这个时候，坏字符 a 在模式串中是存在的，模式串中下标是 0 的位置也是字符 a。这种情况下，我们可以将模式串往后滑动两位，让两个 a 上下对齐，然后再从模式串的末尾字符开始，重新匹配。

2. 好后缀规则

如果好后缀在模式串中不存在可匹配的子串，那在我们一步一步往后滑动模式串的过程中，只要主串中的{u}与模式串有重合，那肯定就无法完全匹配。但是当模式串滑动到前缀与主串中{u}的后缀有部分重合的时候，并且重合的部分相等的时候，就有可能会存在完全匹配的情况。

• KMP算法

KMP 算法是根据三位作者（D.E.Knuth，J.H.Morris 和 V.R.Pratt）的名字来命名的，算法的全称是 Knuth Morris Pratt 算法，简称为 KMP 算法。

对于前缀本身，在它的后缀子串中，查找最长的那个可以跟好前缀的前缀子串匹配的。假设最长的可匹配的那部分前缀子串是{v}，长度是 k。我们把模式串一次性往后滑动 j-k 位，相当于，每次遇到坏字符的时候，我们就把 j 更新为 k，i 不变，然后继续比较。

其实KMP算法就是对于BM算法的进一步优化吧。

12.字典树实现搜索引擎自动提醒功能

Trie 树，也叫“字典树”。顾名思义，它是一个树形结构。它是一种专门处理字符串匹配的数据结构，用来解决在一组字符串集合中快速查找某个字符串的问题

Trie 树的本质，就是利用字符串之间的公共前缀，将重复的前缀合并在一起。

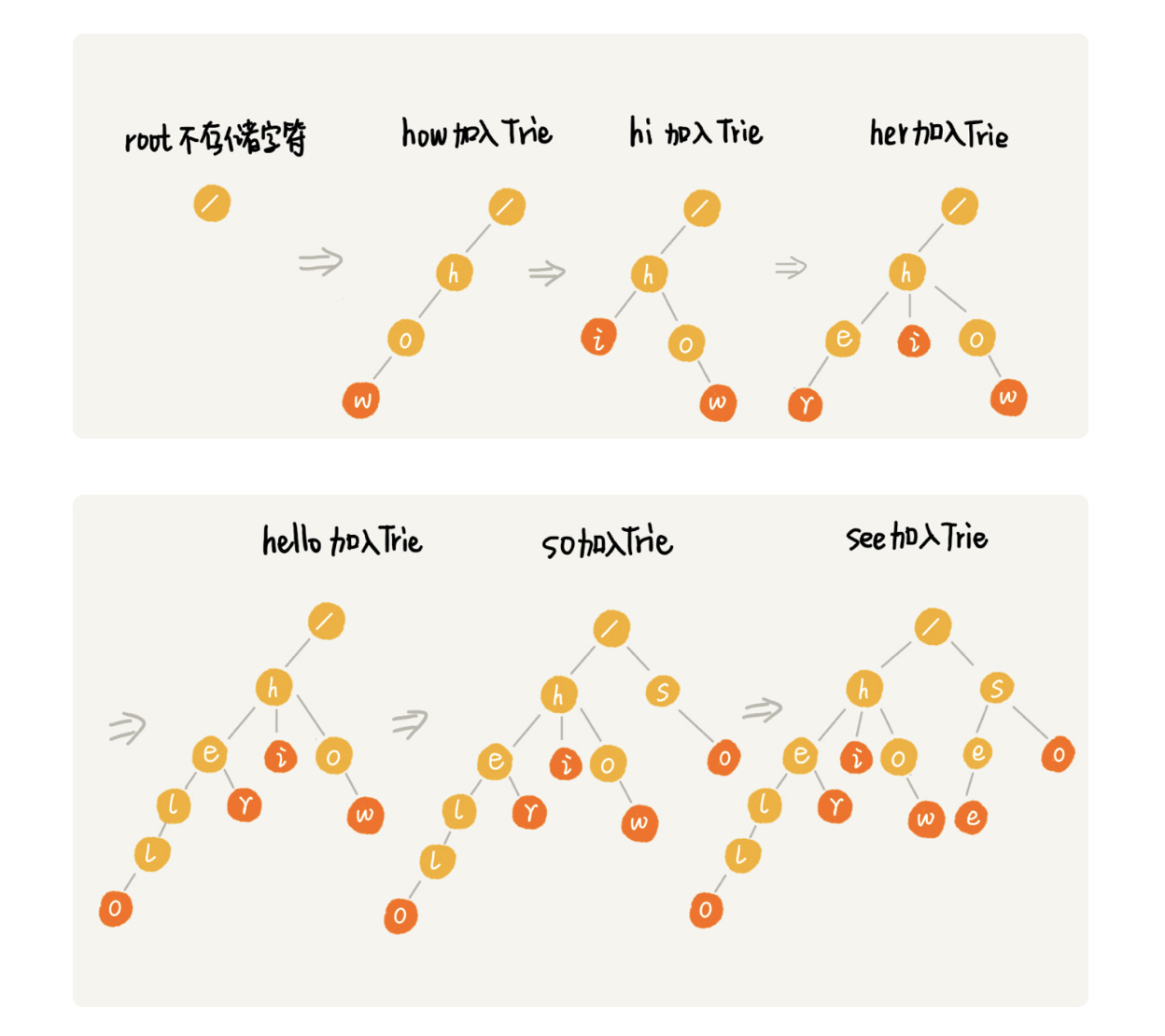
当我们在 Trie 树中查找一个字符串的时候，比如查找字符串“her”，那我们将要查找的字符串分割成单个的字符 h，e，r，然后从 Trie 树的根节点开始匹配。如图所示，绿色的路径就是在 Trie 树中匹配的路径。

在刚刚讲的这个场景，在一组字符串中查找字符串，Trie 树实际上表现得并不好。 它对要处理的字符串有及其严苛的要求。

第一，字符串中包含的字符集不能太大。我们前面讲到，如果字符集太大，那存储空间可能就会浪费很多。即便可以优化，但也要付出牺牲查询、插入效率的代价。

第二，要求字符串的前缀重合比较多，不然空间消耗会变大很多。

第三，如果要用 Trie 树解决问题，那我们就要自己从零开始实现一个 Trie 树，还要保证没有 bug，这个在工程上是将简单问题复杂化，除非必须，一般不建议这样做。

第四，我们知道，通过指针串起来的数据块是不连续的，而 Trie 树中用到了指针，所以，对缓存并不友好，性能上会打个折扣。综合这几点，针对在一组字符串中查找字符串的问题，我们在工程中，更倾向于用散列表或者红黑树。因为这两种数据结构，我们都不需要自己去实现，直接利用编程语言中提供的现成类库就行了。

13.贪心算法的经典运用

分糖果，找零。

14.回溯算法和背包问题

对于每个物品来说，都有两种选择，装进背包或者不装进背包。对于 n 个物品来说，总的装法就有 2^n 种，去掉总重量超过 Wkg 的，从剩下的装法中选择总重量最接近 Wkg 的。

不过，我们如何才能不重复地穷举出这 2^n 种装法呢？这里就可以用回溯的方法。我们可以把物品依次排列，整个问题就分解为了 n 个阶段，每个阶段对应一个物品怎么选择。先对第一个物品进行处理，选择装进去或者不装进去，然后再递归地处理剩下的物品。

正则表达式中，最重要的就是通配符，通配符结合在一起，可以表达非常丰富的语义。为了方便讲解，我假设正则表达式中只包含“”和“?”这两种通配符，并且对这两个通配符的语义稍微做些改变，其中，“”匹配任意多个（大于等于 0 个）任意字符，“?”匹配零个或者一个任意字符。

基于以上背景假设，我们看下，如何用回溯算法，判断一个给定的文本，能否跟给定的正则表达式匹配？我们依次考察正则表达式中的每个字符，当是非通配符时，我们就直接跟文本的字符进行匹配，如果相同，则继续往下处理；如果不同，则回溯。