常见排序算法总结
前置知识
排序算法的种类:
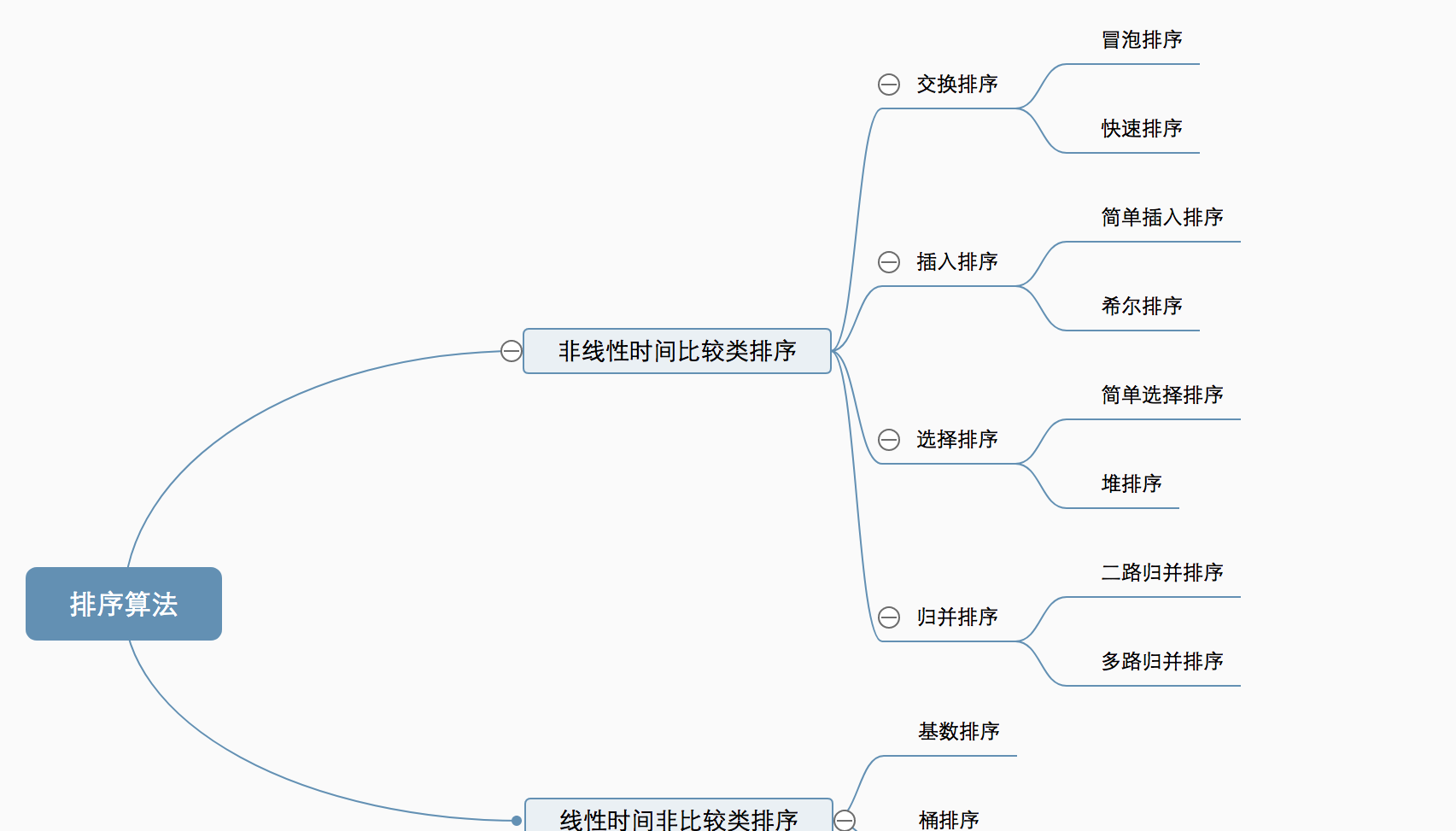
基本知识
- 时间复杂度
一般情况下,算法中基本操作重复执行的次数是问题规模n的某个函数,用T(n)表示,若有某个辅助函数f(n),使得当n趋近于无穷大时,T(n)/f(n)的极限值为不等于零的常数,则称f(n)是T(n)的同数量级函数。记作T(n)=O(f(n)),称O(f(n)) 为算法的渐进时间复杂度,简称时间复杂度。
- 最坏时间复杂度和平均时间复杂度
最坏情况下的时间复杂度称最坏时间复杂度。一般不特别说明,讨论的时间复杂度均是最坏情况下的时间复杂度。
- 空间复杂度
一个程序的空间复杂度是指运行完一个程序所需内存的大小。利用程序的空间复杂度,可以对程序的运行所需要的内存多少有个预先估计。
- 稳定性
所谓稳定性是指待排序的序列中有两元素相等,排序之后它们的先后顺序不变.假如为A1,A2.它们的索引分别为1,2.则排序之后A1,A2的索引仍然是1和2.
稳定也可以理解为一切皆在掌握中,元素的位置处在你在控制中.而不稳定算法有时就有点碰运气,随机的成分.当两元素相等时它们的位置在排序后可能仍然相同.但也可能不同.是未可知的。
可能大部分时候我们不用考虑算法的稳定性.两个元素相等位置是前是后不重要.但有些时候稳定性确实有用处.它体现了程序的健壮性.比如你网站上针对最热门的文章或啥音乐电影之类的进行排名.由于这里排名不会像我们成绩排名会有并列第几名之说.所以出现了元素相等时也会有先后之分.如果添加进新的元素之后又要重新排名了.之前并列名次的最好是依然保持先后顺序才比较好.
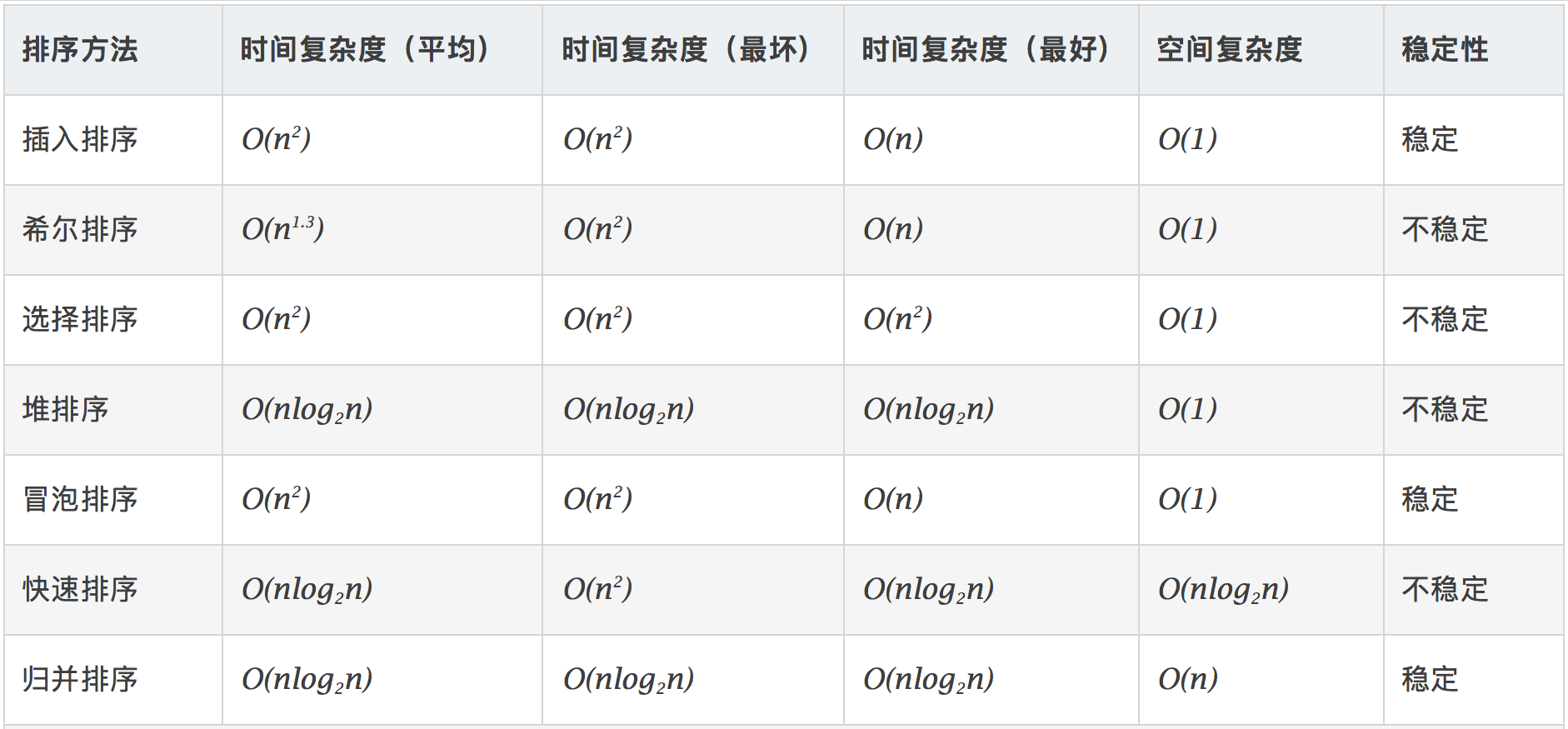
先来张图以便日后查阅
1.冒泡排序
原理
两次循环,外部的循环控制总的循环次数,内部的循环依次比较前后两个元素的大小,并且直接进行交换。
代码
void BubbleSort(int * array,int length)
{
int count = 0;
for(int i=0;i<length;i++)
{
for(int j=0;j<length-1;j++)
{
count ++;
if(array[j]>array[j+1])
{
swap(array[j],array[j+1]);
}
}
}
}
时间复杂度
因为冒泡排序需要开两层循环,第一层是N,第二层是N-1,因此时间复杂度就是O(n^2),并且还是稳定的,最好最坏和平均都是O(n^2)。
稳定性
冒泡是比较两个元素的大小,不相等才会进行交换,这个时候是稳定的。 但可能由于失误,多写了一个等号,这种时候就写成了不稳定的冒泡排序了
优化
- 1.第一趟排序后将10和9交换已经有序,接下来的8趟排序就是多余的,什么也没做。所以我们可以在交换的地方加一个标记,如果那一趟排序没有交换元素,说明这组数据已经有序,不用再继续下去.
void BubbleSort(int arr[], int len)
{
int i = 0;
int tmp = 0;
for (i = 0; i < len - 1; i++)//确定排序趟数
{
int j = 0;
int flag = 0;
for (j = 0; j < len - i - 1; j++)//确定比较次数
{
if (arr[j]>arr[j + 1])
{
//交换
tmp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = tmp;
flag = 1;//加入标记
}
}
if (flag == 0)//如果没有交换过元素,则已经有序
{
return;
}
}
}
- 2.每次不仅仅是从头开始遍历,也会从末尾进行两个元素的比较,而内层循环的遍历只需要取长度的一半,这样会稍微增加效率。
但两种方法最终的时间复杂度,还是O(n^2)
2.插入排序
原理
插入排序又叫直接插入排序,每次选择一个元素,插入到他应该存在的位置。
代码
//插入排序
void InsertionSort(int * array,int length)
{
for(int i=0;i<length;i++)
{
int temp = array[i];
int key = i;
for(int j=i;j<length;j++)
{
if(array[j]<temp)
{
key = j;
temp = array[j];
}
}
while(key >i)
{
swap(array[key],array[key-1]);
key--;
}
}
}
其实,产品经理怎么说,和需求怎么实现是两回事,这里虽然说是插入排序,但仔细分析的话,用swap交换两个元素的位置,反而会方便很多。
时间复杂度
同样是两层循环,我这个写法比冒泡还会稍微慢一点。O(n^2)。
稳定性
稳定,因为可以判断相等的话,不进行插入操作,而是找到不相等的位置,再进行插入。也和程序员的水平有关,若是简单地进行交换,就会写成不稳定的排序算法。(如上)
3.选择排序
原理
每次在未排序的数组中选择一个最小或最大的元素,放到当前的位置,通过两次循环来完成排序,这就是选择排序。
代码
void SelectionSort(int * array,int length)
{
for(int i=0;i<length;i++)
{
int min = i;
for(int j=i;j<length;j++)
{
if(array[min]>array[j])
{
min = j;
}
}
swap(array[i],array[min]);
}
}
时间复杂度
O(n*n)
稳定性
选择排序在不经过特殊处理的情况下,是不稳定的排序算法。因为有相同元素存在的情况下,先排好第一个元素,第二个若不判断大小直接swap,那也是稳定的鸭??
4.桶排序
原理
在C++中,需要待排序的元素都是正数。然后进行以下四个步骤:1.找到这些元素的最大值。2.申请一个数组长度等于最大值+1的数组(为了包括最大值本身)。3.遍历,计算每个下标对应的数出现的次数。4.赋值整个数组的非0的数到待排序数组中。
代码
//桶排序
void BucketSort(int * array,int length)
{
int max = array[0];
for(int i=1;i<length;i++)
{
max = max > array[i] ? max : array[i];
}
int * temp = new int[max+1];
for(int i=0;i<=max;i++)
{
temp[i] = 0;
}
for(int i=0;i<length;i++)
{
temp[array[i]]++;
}
int count=0;
for(int i=0;i<=max;i++)
{
while(temp[i]!=0)
{
array[count] = i;
temp[i]--;
count++;
}
}
delete[] temp;
}
时间复杂度
四次循环,除去可能出现的重复数而进行的循环,都是线性的,O(n)。
稳定性
对于相同的元素而言,在数组前端的会先进入数组,后端的后进入数组,根据数组遍历,也是先进先出,所以怎么就不稳定了??
5.快速排序
原理
快速排序采用分治法,选择数组的第一个元素作为起始点,将比他小的放左边,比他大的放右边。一次循环之后,就生成了左小右大、宏观上有序的数组。
然后进行遍历,直到每次生成的数组都只剩一个元素,无可排序,以达到微观上的有序。
代码
void FastSort(int * array,int left,int right)
{
if (left >= right)
{
return;
}
swap(array[left], array[(left + right) / 2]);
int i = left, j = right, k = array[left];
while (i < j)
{
while (array[j] > k && i < j)
{
j--;
}
array[i++] = array[j];
while (array[i] < k && i < j)
{
i++;
}
array[j--] = array[i];
}
array[(i+j+1)/2] = k;
FastSort(array,left, (i+j+1)/2-1);
FastSort(array,(i+j+1)/2+1, right);
}
时间复杂度
因为是用到了分治法、递归,也有一定的折半思想,故时间复杂度O(n*logn)
快速排序是应用很多的一种排序算法,它虽然不是最快的,但耗时稳定,空间占用也比较平均。
稳定性
不稳定,正因为选择了数组的第一个元素作为初始的比较子,只能控制这个元素相同的值是稳定的,其他元素放入左右的过程中,出现相同的值可能会被打乱顺序。
6.基数排序
原理
以下步骤:1.先计算数组中最大的元素的位数。2.从个位开始排序,一直排到最高位,这样一来就能得到一个有序的数组了。
代码
void RadixSort(int * array,int length)
{
int max = array[0];
for (int i = 1; i < length; i++)
{
if (array[i] > max)
{
max = array[i];
}
}
int d = 0;
while( max > 0 ) {
max /= 10;
d ++;
}
int *tmp = new int[length];
int *count = new int[10]; //计数器
int i, j, k;
int radix = 1;
for(i = 1; i <= d; i++) //进行d次排序
{
for(j = 0; j < 10; j++)
count[j] = 0; //每次分配前清空计数器
for(j = 0; j < length; j++)
{
k = (array[j] / radix) % 10; //统计每个桶中的记录数
count[k]++;
}
for(j = 1; j < 10; j++)
count[j] = count[j - 1] + count[j]; //将tmp中的位置依次分配给每个桶
for(j = length - 1; j >= 0; j--) //将所有桶中记录依次收集到tmp中
{
k = (array[j] / radix) % 10;
tmp[count[k] - 1] = array[j];
count[k]--;
}
for(j = 0; j < length; j++) //将临时数组的内容复制到data中
array[j] = tmp[j];
radix = radix * 10;
}
delete []tmp;
delete []count;
}
时间复杂度
O(n+k),其中k是整数的范围。
稳定性
从最低位开始,是稳定的,从高位开始也可以,但需要比较麻烦的实现。
7.希尔排序
原理
将数组分为多块,每个块进行一次直接插入排序,最后再进行一次直接插入排序。原因也很简单,直接插入排序对数据量少,或者数组基本有序的情况下,是非常快的。
代码
void ShellSort(int * array,int length)
{
for(int gap=length/2;gap>0;gap/=2)
{
// 直接插入排序
for(int i=gap;i<length;++i)
{
int j=i;
while(j-gap>=0 && array[j-gap]>array[j])
{
array[j-gap] = array[j-gap]+array[j];
array[j] = array[j-gap]-array[j];
array[j-gap] = array[j-gap]-array[j];
j=j-gap;
}
}
}
}
时间复杂度
小于O(n^2),大于O(n)
8.计数排序
原理
计数排序有多种说法,在此处我的实现:统计每个数比它出现次数少的数个数,然后就能将这个数放到它应该出现的位置上了。虽然这种方法很慢,很无聊。
代码
void CountingSort(int * array,int length)
{
int * temp = new int[length];
int now;
int count;
for(int i=0;i<length;i++)
{
now = array[i];
count = 0;
for(int j=0;j<length;j++)
{
if(now>array[j])
{
count++;
}
}
temp[count] = now;
}
for(int i=0;i<length;i++)
{
array[i] = temp[i];
}
delete[] temp;
}
时间复杂度
由于本算法的具体含义,和桶排序,基数排序的区别都有些争议,也不好多说什么。在本例中,是O(n^2);
稳定性
本例中,不稳定,因为只是统计了最小值的个数,若存在元素相等时,也是输出多次,已经不是原本的那些数了。
总结
还有堆排序,归并排序,以及一些更加复杂的排序算法,等以后再补充吧!